Algorithmes sur entiers

Algorithmes sur entiers

Créateur de livres
Ajouter cette page à votre livre

Créateur de livres
Retirer cette page de votre livre

La manipulation d'entiers fait l'objet de nombreuses applications en chimie, du fait que les atomes (et isotopes) comptent des nombres entiers de nucléons (nombre de masse), que les molécules (ou ions, complexes) sont constituées d'atomes individuels (cf. formules brutes, indices), que les stœchimétries des réactions impliquent le plus souvent des entiers, que des structures (hélices, cristaux,…) sont caractérisées par des rapports entiers,…

Cette page reprend quelques grands algorithmes classiques sur les nombres entiers, et introduit quelques algorithmes ayant des applications en chimie.

Explication géométrique : en comprenant un nombre entier comme une longueur et un couple d'entiers (a,b) comme un rectangle, leur PGCD est la longueur du côté du plus grand carré permettant de carreler entièrement ce rectangle. L'algorithme d'Euclide décompose ce rectangle en carrés, de plus en plus petits, par divisions euclidiennes successives, de la longueur par la largeur, puis de la largeur par le reste, jusqu'à un reste nul (observez bien ici !). Cela donne ceci en Python :

pgcd.py

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
def gcd(a, b):
    """Calculate the Greatest Common Divisor of a and b.
 
    Unless b==0, the result will have the same sign as b (so that when
    b is divided by it, the result comes out positive).
    """
    while b:
        a, b = b, a%b
    return a
 
n1=210
n2=126
print(gcd(n1, n2))

Si on dispose des décompositions en facteurs premiers d'un nombre entier, on peut aussi établir la valeur du PGCD en effectuant le produit de tous les facteurs communs.

Algorithme d'Euclide
http://stackoverflow.com/questions/11175131/code-for-greatest-common-divisor-in-python
https://docs.python.org/dev/library/fractions.html#fractions.gcd (version incluse dans le langage)
http://en.literateprograms.org/Euclidean_algorithm_%28Python%29 (améliorable !)

Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs (qui sont alors 1 et lui-même) : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …

Pour lister les nombres premiers strictement inférieur à un nombre N donné, un algorithme naïf (appelés tests de primalité) consiste à considérer les naturels un par un, en essayant de le diviser par tous les nombres inférieurs à sa racine carrée : s'il est divisible par l'un d'entre eux, il est composé, et sinon, il est premier. Voici une implémentation en Python de cette idée.

nombres_premiers-01.py

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
Liste de nombres premiers strictement inférieurs à un entier donné
"""
def isprime(n):
    for x in range(2,int(n**0.5)+1):
        if n % x == 0:
            return False
    return True
 
def primelist(n):
    return [a for a in range(2,n) if isprime(a)]
 
p=primelist(1000)
print(p)

L'algorithme peut être rendu plus efficace : il suggère beaucoup de divisions inutiles, par exemple, si un nombre n'est pas divisible par 2, il est inutile de tester s'il est divisible par 4. En fait, il suffit de tester sa divisibilité par tous les nombres premiers inférieurs à sa racine carrée. Le crible d'Ératosthène est une méthode, reposant sur cette idée, qui permet de trouver tous les nombres premiers inférieurs à un certain entier naturel donné N. En supprimant tous les multiples, à la fin il ne restera que les entiers qui ne sont multiples d'aucun entier, et qui sont donc les nombres premiers. Voici une implémentation en Python du crible d'Ératosthène :

nombres_premiers-03.py

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
Liste de nombres premiers strictement inférieurs à un entier donné
"""
def primelist(n):
    """
    Version avec crible d'Eratosthenes
    """
    li = range(n+1)  # création d'une liste d'entiers jusque n
    li[1] = 0        #  0 (déjà à 0) et 1 ne sont pas premiers
    ncur = 2            # prochain nombre à tester
    while ncur ** 2 <= n:  # tant que ncur est inférieur à sqrt(n)
        li[ncur*2::ncur] = [0] * (n // ncur - 1) # éliminer (mettre à 0)
                                          # les multiples de ncur
        # ncur suivant (il ne doit pas être déjà mis à zéro)
        ncur += 1
        while not li[ncur]:
            ncur += 1
    return [a for a in li if a != 0]  # renvoie une liste avec les élements non nuls
 
p=primelist(1000)
print(p)

Version élémentaires, par essais systématiques de diviseurs :

title : factorisation_nombres_premiers-01.py

#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
Factorisation en nombres premiers ; méthode par essais successifs
"""
 
def prime_factors(n):
    li = []
    f = 2  # premier facteur à tester
    while f*f <= n:
        while (n % f) == 0:
            li.append(f)  # on ajoute f à la liste
            n = n/f           # on divise par f
        f = f+1 if f == 2 else f+2  # pour ne pas essayer les nombres pairs
    if n > 1:  # si on n'a pas obtenu n=1, alors le facteur restant est premier
       li.append(n)
    return li
 
 
p=prime_factors(1234567890)
print(p)

Exercices :

amélioration la recherche en combinant l'utilisation du crible d'Eratosthenes
utiliser la décomposition en facteurs premiers de deux nombres (ou plus) pour trouver leur PGCD : pour l'ensemble des facteurs communs aux nombres, il s'agit du produit de ces facteurs élevés à la puissance la plus basse dans les décompositions

Techniques avancées :

Integer factorization
Fast prime factorization module (stackoverflow)
librairie sympy → pip install sympy (ou conda install sympy)
- Use the function sympy.ntheory.factorint : “Given a positive integer n, factorint(n) returns a dict containing the prime factors of n as keys and their respective multiplicities as values.” For example:

from sympy.ntheory import factorint
factorint(10**20+1) → {73: 1, 5964848081: 1, 1676321: 1, 137: 1}

http://stackoverflow.com/questions/16996217/prime-factorization-list
http://en.wikipedia.org/wiki/Talk%3APrime_factorization_algorithm (récursif)
http://rosettacode.org/wiki/Prime_decomposition#Python (avancé)
http://codereview.stackexchange.com/questions/11317/prime-factorization-of-a-number (améliorable)
http://stackoverflow.com/questions/4643647/fast-prime-factorization-module (intéressant)
http://gilles.dubois10.free.fr/Nombres/Naturels/decomposition.html
http://python.jpvweb.com/mesrecettespython/doku.php?id=decomposition_en_facteurs_premiers (améliorable)
http://anh.cs.luc.edu/331/code/factoring.py (intéressant)
http://en.wikipedia.org/wiki/Wheel_factorization
Some code to for teaching primes (génération de figures pour enseigner les nombres premiers)

Explication de la relation entre PGCD et PPCM via les facteurs premiers des nombres (cf. wikipedia) : le PPCM de deux nombres est obtenu par le produit de chacun des facteurs premiers dans la décomposition des deux nombres, élevés à la puissance la plus haute dans ces décompositions. On a alors que le produit des deux nombres équivaut au produit du PGCD par le PPCM et dès lors : PPCM(a,b) = a * b / PGCD(a,b) !

Voici un exemple utilisant les décompositions en facteur premier de 1470 et 252 :

Facteurs premiers de 1470	Facteurs premiers de 252
2	2²
3	3²
5
7²	7

Le PGCD est 42, obtenu par le produit des facteurs communs (soulignés), tandis que le PPCM est obtenu par le produit de tous les facteurs, en utilisant la puissance la plus grande (en gras). Tous les facteurs du tableau de décomposition, soit de la première colonne, soit de la seconde, sont tous utilisés. Par conséquent on a bien pour deux nombres a et b que PPCM(a,b) = a * b / PGCD(a,b) !

Énoncé en version “appliquée” :

La carte des apéritifs propose un certain nombre d’éléments, à des prix différents. Quel assortiment puis-je acheter, coûtant exactement une certaine somme d’argent N ?

Illustration :

En chimie, un problème tout à fait équivalent consiste, en masses entières (donc en nombre de nucléons), à trouver une formule chimique incluant différents atomes d'éléments différents qui donnera une masse entière donnée. En voici une solution :

title : aperitif_initial-02.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
http://paternault.fr/informatique/jouets/aperitif.html
https://git.framasoft.org/spalax/jouets/blob/master/README.rst
https://wiki.python.org/moin/Generators
"""
 
def aperitif(total, prix):
    """Solutions du problème des apéritifs.
 
    version sans itérateur 
 
    :arg total int: Prix total à atteindre.
    :arg prix list: Liste des prix disponibles.
 
    :return: liste des solutions, ces solutions étant des
             listes correspondant à ``prix``.
    """
 
    if len(prix) == 0:
        return []
    if len(prix) == 1:
        if total % prix[0] == 0:
            return [[int(total // prix[0])]]
    liste=[]
    for nombre in range(int((total // prix[0])+1)):
        for solution in aperitif(total - prix[0]*nombre, prix[1:]):
            liste.append([nombre] + solution)
    return liste
 
atomes=[1,12,14,16,32]
# atomes=atomes[::-1]
masse=59
print(atomes,type(atomes))
print(masse, type(masse))
print(aperitif(masse, atomes))

formules CHON(S)
protéines
spectrométrie de masse (en masses entières)

L’énoncé de ce problème extrêmement difficile (un des problèmes de Karp) est par contre simple, faisant référence à un problème courant :

Étant donné plusieurs objets possédant chacun un poids et une valeur et étant donné un poids maximum pour le sac, quels objets faut-il mettre dans le sac de manière à maximiser la valeur totale sans dépasser le poids maximal autorisé pour le sac ?

En voici une illustration (source wikimedia) :

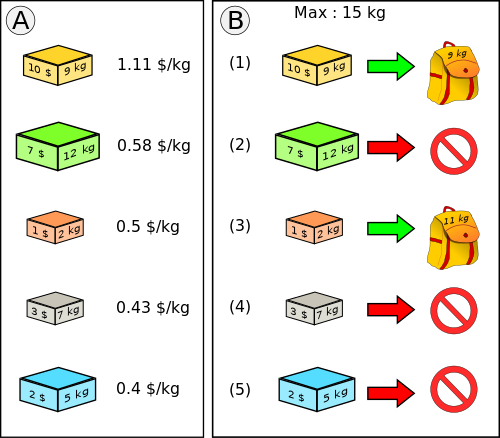
Ce problème revêt une importance économique dans de nombreux secteurs tels que la découpe de matériaux (afin de minimiser les pertes) ou le chargement de cargaisons (avions, camions, bateaux,…). Un examen systématique des possibilités conduit à une explosion combinatoire du nombre de configurations à examiner !

Solutions en Python :