Table des matières
Les bases de NumPy
NumPy est une extension du langage de programmation Python, destinée à manipuler des matrices ou tableaux multidimensionnels ainsi que des fonctions mathématiques opérant sur ces tableaux.
Chaque élément d'un tableau numpy occupe un nombre fixe d'octets, associé à un type particulier de donnée (data-type, ou dtype). Les types les plus courants incluent les entiers, bytes, entiers courts, booléens, nombres en virgule flottante, nombres complexes,…
Numpy permet la manipulations des vecteurs, matrices et polynômes. Un tableau bidimensionnel peut aussi bien représenter une matrice, comme les intensités des pixels d'une image.
Directive d'importation
- standard :
import numpy as np
Tableaux numériques
On convertit facilement des listes Python en tableau numpy. Essayez ceci :
import numpy as np a = np.array([[1,2],[3,4]]) print(a) print(a.dtype)
Sortie :
[[1 2]
[3 4]]
<type 'numpy.ndarray'>
Les fonctions arange et shape sont bien pratiques pour générer des nombres en séquences et réarranger des listes de nombres. La fonction linspace est utile parce qu'elle impose exactement le nombre de valeurs crées ente un minimum et un maximum.
Vous pouvez consulter cette page pour consulter d'autres fonctionnalités, ou cette ancienne documentation.
- arrays_01.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Divers codes à essayer pour créer des tableaux "array" """ import numpy as np a = np.array(((1,2),(3,4))) # on peut créer un "array" à partir d'un tuple # afficher a, le nombre de dimensions, les dimensions, le type de donnée print(a, a.ndim, a.shape, a.dtype) # avec des "floats" : b = np.array([ [1.1, 2.2, 3.3, 4.4], [5.5, 6.6, 7.7, 8.8], [9.9, 0.2, 1.3, 2.4], ]) print(b, b.ndim, b.shape, b.dtype) # un tableau de zéros c = np.zeros((4,2)) print(c, c.ndim, c.shape, c.dtype) # un tableau tridimensionnel de 1 "complexe" d = np.ones((2,3,4),dtype=complex) print(d, d.ndim, d.shape, d.dtype) # un tableau avec arange, et ensuite reshape e1 = np.arange(1,36,1) e = np.reshape(e1,(5,7)) print(e, e.ndim, e.shape, e.dtype) f = np.random.rand(3,3) print(f, f.ndim, f.shape, f.dtype) # utilisation de linspace pour imposer le nombre d'éléments générés : g = np.linspace(0.,np.pi,11) print(g, g.ndim, g.shape, g.dtype)
Quelques manipulations élémentaires :
- arrays_02.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Divers codes à essayer pour manipuler des tableaux "array" """ import numpy as np a = np.array([[1,2],[3,4]]) b = np.array([[1,1],[1,1]]) c = a + b # addition terme à terme print(c, c.ndim, c.shape, c.dtype) d =a * b # multiplication terme à terme print(d, d.ndim, d.shape, d.dtype) e = np.dot(a,b) # multiplication matricielle print(e, e.ndim, e.shape, e.dtype) f = np.sin(np.pi*0.5*a) # fonction mathématique et adaptation automatique du type print(f, f.ndim, f.shape, f.dtype) g = np.transpose(a) # transposition print(g, g.ndim, g.shape, g.dtype) print(np.sum(a),np.min(a), np.max(a)) # somme des éléments, minimum, maximum
Fonctions mathématiques principales :
- abs, sign, sqrt
- logarithmes/exponentielles : log, log10, exp
- trigonométriques et inverses : sin, cos, tan, arcsin, arccos, arctan
- hyperboliques et inverses : sinh, cosh, tanh, arcsinh, arccosh, arctanh
- entiers inférieur, supérieur ou le plus proche : floor, ceil, rint
Autres fonctions
- min et max rendent le minimum et le maximum, argmin et argmax rendent les indices de ce éléments dans un tableau 1D (consulter la documentation pour les dimensions supérieures).
- sorted : tri
- clip : cliping permettant d'éliminer des valeurs inférieures à une borne minimale donnée ou supérieures à une borne maximale
- unique : élimine les “doublons”
- fonctions booléennes, pour des conditions, ou pour filtrer suivant des conditions (voir la documentation)
- copy : copie d'un tableau (pour éviter les modifications lors d'utilisation directe ou par référence)
- .tolist() : convertit un tableau numpy en liste standard de python
Algèbre linéaire
- simple_linear_system.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Solve a system of simultaneous equation in two variables of the form 2 * x + 7 * y = 17. 3 * x - 5 * y = -21. reference : http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.solve.html """ # import numpy as np a = np.array([[2.,7.],[3.,-5.]]) # coefs matrice b = np.array([[17.],[-21.]]) # independent coef vector print(np.linalg.solve(a,b)) # solution
Quelques possibilités supplémentaires :
- arrays_linalg_03.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Divers codes à essayer pour de l'algèbre linéaire avec des tableaux "array" """ import numpy as np a = np.array([[1,2],[3,4]]) print(a, a.ndim, a.shape, a.dtype) b = np.linalg.inv(a) # matrice inverse print(b, b.ndim, b.shape, b.dtype) unit = np.eye(2) # matrice unitaire print(unit, unit.ndim, unit.shape, unit.dtype) v = np.array([[10.], [14.]]) # vecteur colonne x1 = np.dot(b,v) # multiplication de l'inverse de a par v x2 = np.linalg.solve(a,v) # solution du système linéaire de coefficients # des inconnues a et de coefficients indépendants b # les deux techniques donnent évidemment le même résultat ! print(x1, x1.ndim, x1.shape, x1.dtype) print(x2, x2.ndim, x2.shape, x2.dtype) # valeurs propres et vecteurs propres de matrices : d = np.array([[1,1],[-1,1]]) print(np.linalg.eig(d))
Numpy dispose aussi d'une classe particulière de “arrays” pour des matrices.
Autres fonctions
- inner : produit scalaire (équivalent à dot sur des tableaux 1D)
- cross : produit vectoriel
- det : déterminant
Statistiques élémentaires
- arrays_stats_elem_04.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Divers codes à essayer pour des statistiques élémentaires sur des tableaux "array" """ import numpy as np a = np.array([1.,2.,3.5,5.,6.,7.,7.4,7.8,8.2,8.4,8.5,9.,10.2,12.5]) print(a, a.ndim, a.shape, a.dtype) print("médiane = ",np.median(a)) print("moyenne = ",np.mean(a)) print("variance = ",np.var(a)) print("Écart-type = ",np.std(a))
Références complémentaires
Itérations sur les tableaux
- arrays_iteration_05.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ itérations sur des tableaux "array" """ import numpy as np a = np.array([1.,2.,3.5,5.,6.,7.,7.4,7.8,8.2,8.4,8.5,9.,10.2,12.5]) for x in a: print(x) # l'itération sur un tableau multdimensionnel se fait sur un premier niveau de sous-listes b = np.array([ [1.1, 2.2, 3.3, 4.4], [5.5, 6.6, 7.7, 8.8], [9.9, 0.2, 1.3, 2.4], ]) for x in b: print(x) for y in x: print(y,", ",) print
Manipulation de polynômes
poly1d & polynomial ordonnent les coefficients en sens inverses !!!
- arrays_polynomes_06.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Utilisation de tableaux "array" pour des polynômes """ import numpy as np from numpy.polynomial import Polynomial as P # les coefficients du polynômes sont donnés par ordre décroissance des dégrés a = P([4., 3., 2., 1.]) # = x³ + 2x² + 3x + 4 print("polynôme : \n", a, type(a)) # les coefficients de a : print("coefficients : ", a.coef) # les racines de a : print("racines : ", a.roots()) # l'ordre du polynôme : print("ordre : ", a.degree()) # évaluations sur un vecteur x = np.linspace(0, 2., 21) print("x = ", x) print("évaluation en x : ", a(x)) # dérivation print("dérivée : \n", a.deriv(1)) print("dérivée seconde : \n", a.deriv(2)) print("dérivée troisième : \n", a.deriv(3)) print("dérivée quatrième : \n", a.deriv(4)) # intégration print("intégrale : \n", a.integ(1)) # création d'un polynôme par ses racines b = a.roots() c = P.fromroots(b) print("Polynômes recrées par les racines :\n", c) # # fitting polynomial # # utilisation de poly1d (ancienne librairie) # # numpy.polyfit (poly1d) : # https://docs.scipy.org/doc/numpy/reference/routines.polynomials.poly1d.html # https://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html # xd = np.array([0., 1., 2., 3., 4., 5.]) yd = np.array([0.05, 0.99, 3.95, 9.17, 15.86, 24.93]) pfit = np.poly1d(np.polyfit(xd, yd, 2)) print("fit d'une parabole (polynôme d'ordre 2) sur ces x et y :") print(xd) print(yd) print("polynôme de fit : \n", pfit) # # "Unfortunately, np.polynomial.polynomial.polyfit returns the coefficients # in the opposite order of that for np.polyfit and np.polyval" # → https://stackoverflow.com/questions/18767523/fitting-data-with-numpy # ################################################## # Ajouter les fits utilisant numpy.polynomial... # ################################################## # # numpy.polynomial.polynomial.Polynomial.fit : # https://docs.scipy.org/doc/numpy/reference/routines.polynomials.html # https://docs.scipy.org/doc/numpy/reference/routines.polynomials.package.html # https://docs.scipy.org/doc/numpy/reference/routines.polynomials.classes.html # https://docs.scipy.org/doc/numpy/reference/generated/numpy.polynomial.polynomial.Polynomial.fit.html # # numpy.polynomial.polynomial.polyfit : # https://docs.scipy.org/doc/numpy/reference/generated/numpy.polynomial.polynomial.polyfit.html #
Autres fonctions : voir ici
L'ordre des coefficients peut facilement être inversé par un slice avec les paramètres [::-1]
Transformées de Fourier
Le module de transformée de Fourier discrète de numpy comprend de nombreuses variantes, et les transformées peuvent aussi être effectuées via le module équivalent fftpack de Scipy.
- fonctions-FT-04.py
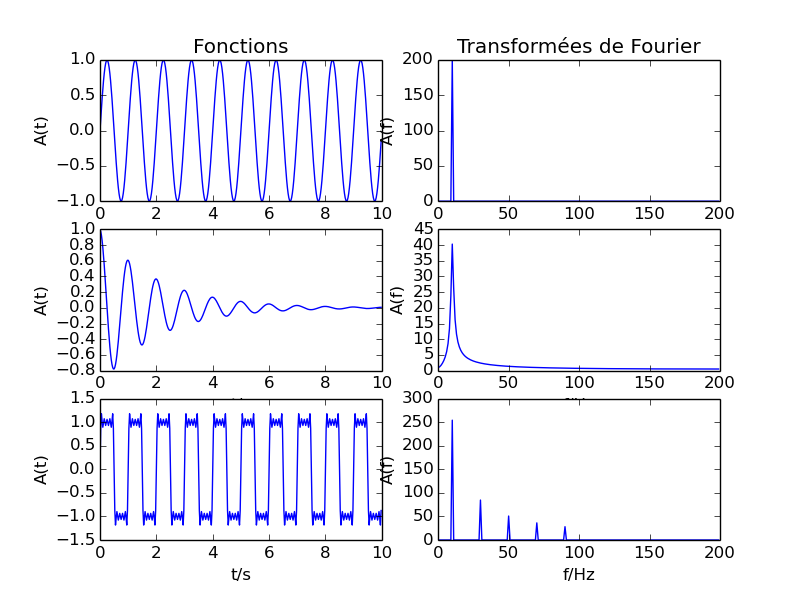
#!/usr/bin/env python #-*- coding: utf-8 -*- # graphes de fonctions et des transformées de Fourier, utilisant numpy # et matplotlib pour les graphes import numpy as np # directive d'importation standard de numpy from numpy import fft # importation spécifique du module fft de numpy import matplotlib.pyplot as plt #from scipy import fftpack # directive d'importation standard du module équivalent de scipy # https://docs.scipy.org/doc/scipy-0.15.1/reference/api.html#guidelines-for-importing-functions-from-scipy #from pylab import * # directive d'importation alternative en mode "pylab" --> supprimer les plt., fft., def f1(t): f = np.sin(np.pi*2.*t) return f def f2(t): f = np.exp(-t/2.)*np.cos(np.pi*2.*t) return f def f3(t): f = (4./np.pi)*(np.sin(np.pi*2.*t)+np.sin(np.pi*6.*t)/3.+np.sin(np.pi*10.*t)/5.+np.sin(np.pi*14.*t)/7.+np.sin(np.pi*18.*t)/9.) return f # une TF peut se faire via : # fft.fft() du fait de la directive from numpy import fft # , ou np.fft.fft() du fait de import numpy as np # , ou fftpack.fft(y1) si on utilise le module de scipy x = np.arange(0.0,10.0,0.025) y1 = f1(x) z1 = fft.fft(y1) w1 = np.abs(z1[:len(z1)//2]) y2 = f2(x) z2 = fft.fft(y2) w2 = np.abs(z2[:len(z2)//2]) y3 = f3(x) z3 = fft.fft(y3) w3 = np.abs(z3[:len(z3)//2]) # doc subplot : http://matplotlib.org/api/pyplot_api.html?highlight=subplot#matplotlib.pyplot.subplot plt.subplot(3,2,1) # sous-graphes en 3 lignes et 2 colonnes, graphe 1 plt.title('Fonctions') plt.plot(x,y1) plt.xlabel("t/s") plt.ylabel("A(t)") plt.subplot(3,2,2) # sous-graphes en 3 lignes et 2 colonnes, graphe 2 plt.title(u'Transformées de Fourier') plt.plot(w1) plt.xlabel("f/Hz") plt.ylabel("A(f)") plt.subplot(3,2,3) # sous-graphes en 3 lignes et 2 colonnes, graphe 3 plt.plot(x,y2) plt.xlabel("t/s") plt.ylabel("A(t)") plt.subplot(3,2,4) # sous-graphes en 3 lignes et 2 colonnes, graphe 4 plt.plot(w2) plt.xlabel("f/Hz") plt.ylabel("A(f)") plt.subplot(3,2,5) # sous-graphes en 3 lignes et 2 colonnes, graphe 5 plt.plot(x,y3) plt.xlabel("t/s") plt.ylabel("A(t)") plt.subplot(3,2,6) # sous-graphes en 3 lignes et 2 colonnes, graphe 6 plt.plot(w3) plt.xlabel("f/Hz") plt.ylabel("A(f)") plt.savefig('fonctions-fft.png') plt.show()
Figure obtenue :
Avantages de numpy
L'utilisation de la librairie nump permet souvent d'améliorer les performances par rapport à un code numérique écrit en “pure Python”. Voici un exemple :
- direct_pi_multirun-timeit.py
# -*- coding: utf-8 -*- """ In the introduction of his MOOC "SMAC" (Statistical Mechanics: Algorithms and Computations - https://www.coursera.org/learn/statistical-mechanics), Werner Krauth propose a simple method to compute pi using a direct sampling Monte Carlo simulation. A program is proposed in Python, in a version which allows to do many runs of the function direct_pi(N). The code is written in a style close to pseudocode used for algorithms, or classical coding style used in C, Fortran,... It is possible to write the function in a more "pythonic" way, or to use the numpy numerical library, to improve compactness and efficiency. Function direct_pi_DV(N) use pure python with list comprehension to eliminate the for loop. The sum is directly made on the boolean comparison results to count the number of true trials. Function direct_pi_DV_np(N) use the numpy library to vectorize the loop, directly square values and sum the array elements over the smaller axis. Again the sum is directly made on the boolean comparisons. Finally, in order to compare efficiency, the execution times of the three versions have been measured using the timeit library. Here is value obtain for a sample run : direct_pi : 3.5209695600005944 s direct_pi_DV : 4.000994963998892 s direct_pi_Dv_np : 0.19237353700009407 s The use ot the numpy library clearly improve the computer speed performance by a factor about 20. """ import random, timeit import numpy as np def direct_pi(N): n_hits = 0 for i in range(N): x, y = random.uniform(-1.0, 1.0), random.uniform(-1.0, 1.0) if x ** 2 + y ** 2 < 1.0: n_hits += 1 return n_hits def direct_pi_DV(N): return sum((random.uniform(-1,1)**2 + random.uniform(-1,1)**2) < 1 for i in range(N)) def direct_pi_DV_np(N): return np.sum((np.random.uniform(-1,1,(N,2))**2).sum(1)<1) n_runs = 1000 n_trials = 4000 # running : for run in range(n_runs): print(run, 4.0 * direct_pi(n_trials) / n_trials) for run in range(n_runs): print(run, 4.0 * direct_pi_DV(n_trials) / n_trials) for run in range(n_runs): print(run, 4.0 * direct_pi_DV_np(n_trials) / n_trials) # timing three versions : print(timeit.timeit('direct_pi('+str(n_trials)+')', "from __main__ import direct_pi", number=n_runs)) print(timeit.timeit('direct_pi_DV('+str(n_trials)+')', "from __main__ import direct_pi_DV", number=n_runs)) print(timeit.timeit('direct_pi_DV_np('+str(n_trials)+')', "from __main__ import direct_pi_DV_np", number=n_runs))
Références
- NumPy: creating and manipulating numerical data, de Emmanuelle Gouillart, Didrik Pinte, Gaël Varoquaux, and Pauli Virtanen
- Array programming with NumPy Harris, C.R., Millman, K.J., van der Walt, S.J. et al., Nature 585, 357–362 (2020) DOI: 10.1038/s41586-020-2649-2
- What is timeit module in Python? Chetan Ambi, 02/02/2022 (mesure du temps d'exécution avec la librairie timeit)