Suite de Fibonacci : un premier programme
Voici un embryon non fonctionnel de programme. Il y manque alors des éléments (à la place des “???”)
- fibonacci02-sur_la_piste.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Calculs des premiers éléments de la suite de Fibonacci. Référence : http://fr.wikipedia.org/wiki/Suite_de_Fibonacci """ # élément d'indice 0 i = 0 a = 0 print(i,a) # élément d'indice 1 i = 1 b = 1 print(i,b) # structure de répétition pour appliquer la règle de récurrence max = 100 # indice du dernier terme (ou presque) while ??? < max: # il faut calculer les indices et éléments suivants de la suite # et poursuivre avec les mêmes instructions ??? print(i,c) #quelque chose de ce genre
Un peu de réflexion pour se rendre compte qu'il faut comparer i à max, mais surtout qu'il faudra actualiser i, calculer le nouvel élément de la suite par la relation de récurrence et surtout remettre dans les variables a et b des éléments actualisés (nouveaux, ou décalés dans la file d'une position).
On propose alors ceci :
- fibonacci03-fonctionnel.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Calculs des premiers éléments de la suite de Fibonacci. Référence : http://fr.wikipedia.org/wiki/Suite_de_Fibonacci """ # élément d'indice 0 i = 0 a = 0 print(i,a) # élément d'indice 1 i = 1 b = 1 print(i,b) # structure de répétition pour appliquer la règle de récurrence max = 100 # indice du dernier terme (ou presque) while i < max: # il faut calculer les indices et éléments suivants de la suite # et poursuivre avec les mêmes instructions c = a + b i = i + 1 print(i,c) a = b b = c
Mais avons-nous terminé ? Ce programme a-t-il toutes les caractéristiques d'un code Python utile ?
Non, car il ne fait que la sortie d'une série d'élément !
Il faudrait créer des fonctions utiles, dans la perspective de pouvoir les insérer dans des programmes plus vastes. Par exemple :
- une fonction fibonacci-element(i) qui donne l'élément i de la suite
- une fonction fibonacci-liste(n) qui donne tous les éléments de la suite jusqu'à l'élément n
- une fonction fibonacci-indice(nombre) qui donne l'indice de l'élément de valeur nombre, ou les deux indices dont les éléments sont les plus proches qui encadrent ce nombre.
- …
En guise de préambule, on peut aussi regarder comment rendre un code python plus compact en groupant les commentaires avec les instructions, et en utilisant les affectations multiples (un signe “=” pour des affectations à plusieurs variables séparées par des virgules). Voilà ce que cela donne 1)
- fibonacci04-compact.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Calculs des premiers éléments de la suite de Fibonacci. Référence : http://fr.wikipedia.org/wiki/Suite_de_Fibonacci """ i, a = 0, 0 # élément d'indice 0 print(i,a) i, b = 1, 1 # élément d'indice 1 print(i,b) max = 100 # indice du dernier terme (ou presque) while i < max: # structure de répétition pour appliquer la règle de récurrence # indices et éléments suivants de la suite i, c = i+1, a+b print(i,c) a, b = b, c
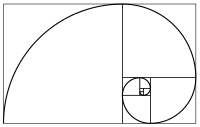 On peut utiliser le module turtle pour représenter un début de la spirale de Fibonacci. Il suffit d'ajouter quelque lignes au programme :
On peut utiliser le module turtle pour représenter un début de la spirale de Fibonacci. Il suffit d'ajouter quelque lignes au programme :
- fibonacci-turtle.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Calculs des premiers éléments de la suite de Fibonacci. Référence : http://fr.wikipedia.org/wiki/Suite_de_Fibonacci Représentation en spirale utilisant turtle """ from turtle import * reset() up() forward(50) down() scale = 2 i, a = 0, 0 # élément d'indice 0 print(i,a) i, b = 1, 1 # élément d'indice 1 print(i,b) max = 12 # indice du dernier terme (ou presque) while i < max: # structure de répétition pour appliquer la règle de récurrence # indices et éléments suivants de la suite i, c = i+1, a+b print(i,c) a, b = b, c # xturtle moves : circle(c*scale,90) input('Tapez sur une touche pour arrêter !')
Pour l'écriture de fonctions, allez à la page suivante !