Table des matières
Potentiel de Morse
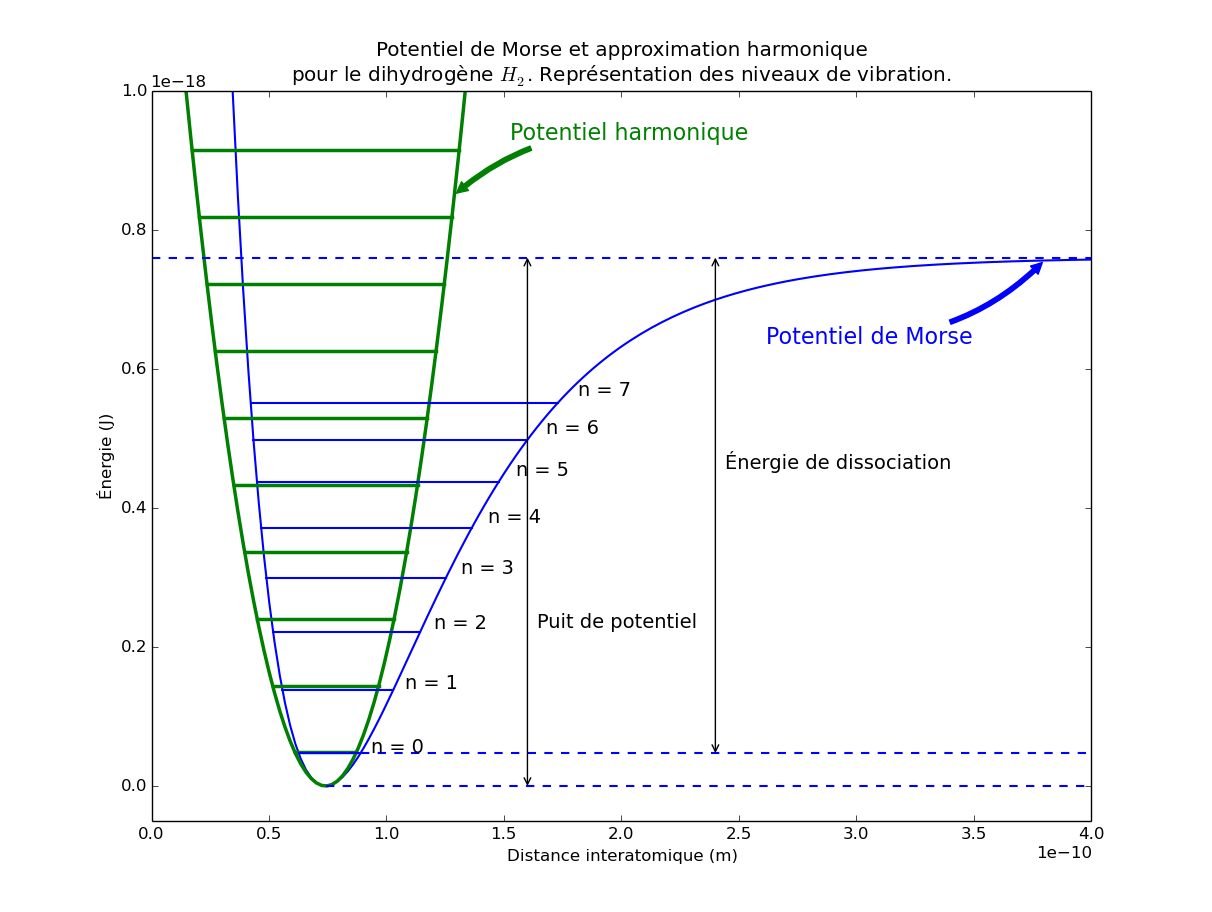
Potentiel de Morse et approximation harmonique, avec représentation des niveaux d'énergie des modèles quantiques correspondants.
Code source :
- potentiel_Morse-04.py
#! /usr/bin/env python # -*- coding: utf-8 -*- """ Représentation du potentiel de Morse pour H2 http://en.wikipedia.org/wiki/Morse_potential http://en.wikipedia.org/wiki/Quantum_harmonic_oscillator approximation harmonique D_e = 7.6E-19 J a = 19.3E-15 m r_e= 74.1E-12 m dérivée de seconde d2V/dr2 = 2 * D_e * a**2. """ import matplotlib.pyplot as plt # directive d'importation standard de Matplotlib import numpy as np # directive d'importation standard de numpy def V(r): # potentiel de Morse return D_e * (1.- np.exp(-a*(r-r_e)))**2. def Vh(r): # potentiel harmonique return D_e * (a*(r-r_e))**2. a = 19.3E9 # en unité m-1 # paramètre de contrôle de la largeur du potentiel r_e = 74.1E-12 # en unité m # distance interatomique d'équilibre (longueur de liaison) #a = 19.3E-3 # en unité pm-1 #r_e = 74.1 # en unité pm D_e = 7.6E-19 # J # énergie de dissociation NA = 6.02214129E23 # nombre d'Avogadro h = 1.054571726E-34 # constante de Planck mH = 1.007825E-3/NA # masse de l'hydrogène nu0 = (a/2.*np.pi)*np.sqrt(2.*D_e/mH) hnu0 = h * nu0 # quantum d'énergie plt.figure(figsize=(12, 9), dpi=80) plt.title(u"Potentiel de Morse et approximation harmonique\npour le dihydrogène $H_2$. Représentation des niveaux de vibration.") r = np.linspace(10.,400.,176) * 1E-12 u,uh = V(r),Vh(r) plt.plot(r,u, color="blue", linewidth=1.5, linestyle="-") plt.plot(r,uh, color="green", linewidth=2.5, linestyle="-") xmax = 400.E-12 plt.xlim(0., xmax) ymax = 1.E-18 plt.ylim(-0.5e-19, ymax) plt.xlabel(u"Distance interatomique (m)") plt.ylabel(u"Énergie (J)") # annotations des courbes xy_annoth = (r_e+np.sqrt(ymax*0.85/(D_e*a**2.)),ymax*0.85) plt.annotate(r'Potentiel harmonique', xy=xy_annoth, xycoords='data', xytext=(+40, +40), textcoords='offset points', fontsize=16, color="green", arrowprops=dict(arrowstyle="simple", connectionstyle="arc3,rad=.2",color="green")) xy_annotm = (xmax*0.95,V(xmax*0.95)) plt.annotate(r'Potentiel de Morse', xy=xy_annotm, xycoords='data', xytext=(-200, -60), textcoords='offset points', fontsize=16, color="blue", arrowprops=dict(arrowstyle="simple", connectionstyle="arc3,rad=.2",color="blue")) # description du puit de potentiel plt.plot((r_e,xmax),(0,0), color="blue", linewidth=1.5, linestyle="--") plt.plot((0.,xmax),(D_e,D_e), color="blue", linewidth=1.5, linestyle="--") plt.annotate("", xy=(xmax*0.4,0.), xytext=(xmax*0.4,D_e), arrowprops=dict(arrowstyle="<->",color='k',shrinkA=0,shrinkB=0)) plt.text(xmax*0.41, D_e*0.3, u"Puit de potentiel", fontsize=14) # niveaux de vibrations de l'approximation harmonique : for v in range(10): E = hnu0*(v+0.5) dr = np.sqrt(E/(D_e*a**2.)) plt.plot([r_e-dr,r_e+dr],[E,E], color="green", linewidth=2.5, linestyle="-") # niveaux de vibrations du potentiel de Morse : #vmax = int((2.*D_e-hnu0)/hnu0) # valeur maximale de v suivant la théorie vmax = 8 # compromis pour la représentation for v in range(vmax): E = hnu0*(v+0.5) - (hnu0*(v+0.5))**2/(4.*D_e) r1,r2 = r_e-np.log(1.+np.sqrt(E/D_e))/a,r_e-np.log(1.-np.sqrt(E/D_e))/a plt.plot([r1,r2],[E,E], color="blue", linewidth=1.5, linestyle="-") # description de l'énergie de dissociation (niveau de vibration 0) if v == 0: plt.plot((r2,xmax),(E,E), color="blue", linewidth=1.5, linestyle="--") plt.annotate("", xy=(xmax*0.6,E), xytext=(xmax*0.6,D_e), arrowprops=dict(arrowstyle="<->",color='k',shrinkA=0,shrinkB=0)) plt.text(xmax*0.61, D_e*0.6, u"Énergie de dissociation", fontsize=14) # numérotation des niveaux de vibration plt.text(r2*1.05, E*1.02, "n = "+str(v), fontsize=14) #print(v,E) plt.show()
Figure :
Prolongement
- ajouter des annotations comme la distance interatomique d'équilibre
- Représenter dynamiquement l'oscillation de la longueur de liaison en intégrant les équations du mouvement. La force doit être calculée à partir du potentiel.
Références
- Article original : Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels Philip M. Morse, Phys. Rev. 34, 57 – Published 1 July 1929. DOI : http://dx.doi.org/10.1103/PhysRev.34.57