Table des matières
Ceci est une ancienne révision du document !
Surface d'énergie potentielle
Historique
Eyring et Polanyi ont publié en 1931 l'article On Simple Gas Reactions dans lequel ils décrivent les trajets des atomes dans la réaction H2 + H –> H + H2 (échange d'atomes). Ces travaux aboutiront au développement des notions de complexe activé (activated complex) ou état de transition (transition state).
Représentation graphique
L'article “On a New Method of Drawing the Potential Energy Surface” (Shin Sato, J. Chem. Phys. 23, 592, 1955) présente une simplification relativement facile à mettre en oeuvre dans le cas où les 3 atomes d'hydrogène sont alignés.
Des expression analytiques sont proposées pour un état d'énergie liant et un état d'énergie non-liant :
- $E_{bond}= D_e [\exp(-2\beta(r-r_e))-2\exp(-\beta(r-r_e))]$
- $E_{ant}= \frac{D_e}{2} [\exp(-2\beta(r-r_e))+2\exp(-\beta(r-r_e))]$
$r_e$ est la distance interatomique d'équilibre de H2, $D_e$ la profondeur du puits de potentiel et $\beta$ un paramètre pour ajuster sa largeur (voir le Potentiel de Morse, et l'approximation harmonique).
Pour 2 atomes d'hydrogène A et B, une approximation est :
- $E_{bond}= \frac{Q_{AB}+\alpha_{AB}}{1+S^2_{AB}} = \frac{Q_{AB}+\alpha_{AB}}{1+k}$
- $E_{ant}= \frac{Q_{AB}-\alpha_{AB}}{1-S^2_{AB}} = \frac{Q_{AB}-\alpha_{AB}}{1-k}$
Où $k=S^2_{AB}$ et $Q_{AB}$, $\alpha_{AB}$ et $S_{AB}$ sont respectivement les intégrales de coulomb, d'échange et de recouvrement, toutes fonctions de la distance $r_{AB}$ entre les atomes A et B.
La solution proposée par Sato pour 3 atomes A, B, C, avec l'hypothèse $S^2_{AB}=S^2_{BC}=S^2_{CA}=k$ est :
- $E = \frac{1}{1+k} \{ Q_{AB} + Q_{BC} + Q_{CA} - \sqrt{\frac{2}{1}[(\alpha_{AB} - \alpha_{BC})^2 + (\alpha_{BC} - \alpha_{CA})^2 + (\alpha_{CA} - \alpha_{AB})^2 ]} \}$
On obtient facilement $Q_{AB}$ et $\alpha_{AB}$ :
- $Q_{AB} = ((1+k)E_{bond} + (1-k)E_{ant}) / 2$
- $\alpha_{AB} = ((1+k)E_{bond} - (1-k)E_{ant}) / 2$
Sato présente des PES avec l'hypothèse k = 0.18 pour des distances jusque 0.5 nm.
Programme
<sxh python; title : PES-contour-01.py> #!/usr/bin/env python # -*- coding: utf-8 -*- “”“ Tracés de lignes de niveau ou isolignes Application : Potentiel Energy Surface de la réaction H + H2 –> H2 + H
”“” # ref : http://bulldog2.redlands.edu/facultyfolder/deweerd/tutorials/Tutorial-ContourPlot.pdf
import matplotlib.pyplot as plt # directive d'importation standard de Matplotlib import numpy as np # directive d'importation standard de numpy from mpl_toolkits.mplot3d import Axes3D # Axes3D
def Ebond(rAB):
return D_e * (np.exp(-2.*beta*(rAB-r_e)) - 2.*np.exp(-beta*(rAB-r_e)))
def Eant(rAB):
return 0.5 * D_e * (np.exp(-2.*beta*(rAB-r_e)) + 2.*np.exp(-beta*(rAB-r_e)))
def Q(rAB):
return 0.5 * ((1.+k)*Ebond(rAB) + (1.-k)*Eant(rAB))
def a(rAB):
return 0.5 * ((1.+k)*Ebond(rAB) - (1.-k)*Eant(rAB))
beta=19.3E-3 # pm-1 r_e=74.1 # pm D_e = .76 # E-18 J k=0.18 rmin=10. rmax=400. num=100 x_1d = np.linspace(rmin,rmax, num) print x_1d.shape, x_1d.dtype, x_1d.ndim y_1d = np.linspace(rmin,rmax, num) print y_1d.shape, y_1d.dtype, y_1d.ndim X, Y = np.meshgrid(x_1d, y_1d) print X.shape, X.dtype, X.ndim, Y.shape, Y.dtype, Y.ndim E=(Q(X)+Q(Y)+Q(X+Y)-np.sqrt(2.*1)2.+(a(Y)-a(X+Y))2.+(a(X+Y)-a(X))**2.)))/(1.+k) print np.min(E) #valeur minimale de E
fig = plt.figure(figsize=(12, 12), dpi=80) ax = fig.add_subplot(111) # cf. http://stackoverflow.com/questions/7965743/how-can-i-set-the-aspect-ratio-in-matplotlib ax.set_aspect(“equal”) levels = np.linspace(-1.7, 1.0, 53) CS1 = plt.contour(X, Y, E, levels, colors='k') plt.clabel(CS1, colors = 'k', fmt = '%2.2f', fontsize=14) CS2 = plt.contourf(X, Y, E, levels) #plt.colorbar(CS2) # visualisation éventuelle de l'échelle de couleur
plt.title('Isolignes') plt.xlabel('x (pm)') plt.ylabel('y (pm)')
fig = plt.figure(2,figsize=(15, 15)) ax = Axes3D(fig) ax.plot_surface(X,Y,E, rstride=1,cstride=1 ,cmap=plt.cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('E') plt.show() </sxh>
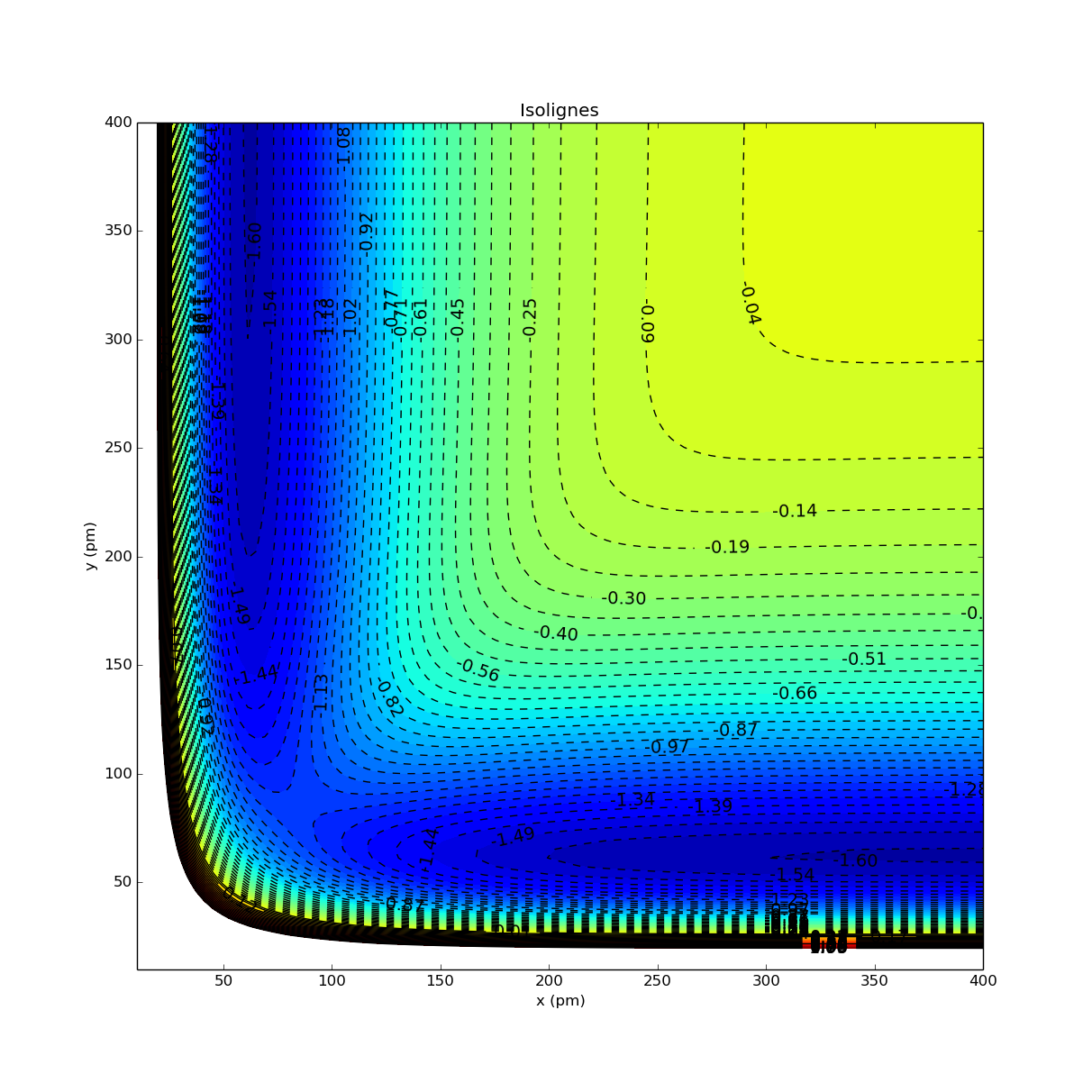
Avec les paramètres essayés, la valeur minimale de E est environ -1.603
Sorties graphiques
Lignes de contour
Surface 3D
Références
- http://www.wag.caltech.edu/home/jsu/Summary/GroundStateExamples.html (réaction H2 + H)
- http://www.personal.psu.edu/jba/publications/articles/23.pdf (HF + H –> H2 + F)
- On a New Method of Drawing the Potential Energy Surface, Shin Sato, J. Chem. Phys. 23, 592 (1955)
- Introduction to potential energy surfaces and graphical interpretation, Ralph Jaquet (2002)
- QUANTENMECHANISCHE DEUTUNG DES VORGANGS DER AKTIVIERUNG F. London Zeitschrift für Elektrochemie und angewandte physikalische Chemie. Volume 35, Issue 9, pages 552–555, September 1929
- W H Miller, Recent Advances in Quantum Mechanical Reactive Scattering Theory, Including Comparison of Recent Experiments with Rigorous Calculations of State-to-State Cross Sections for the H/D+H2→H2/HD+H Reactions, Annual Review of Physical Chemistry, Vol. 41: 245-281 (Volume publication date October 1990) DOI: 10.1146/annurev.pc.41.100190.001333
- Peterson, Kirk A., Woon, David E., Dunning, Thom H. , Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H+H2→H2+H reaction, Journal of Chemical Physics. 5/15/1994, Vol. 100 Issue 10, p7410
Voir aussi :