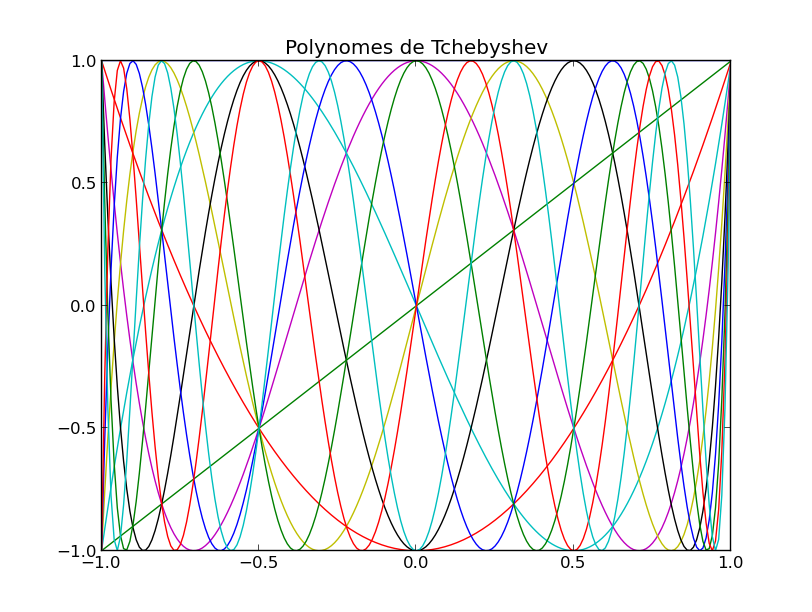
Graphe d'une famille de polynômes orthogonaux
Voici un programme permettant de visualiser les premiers polynômes orthogonaux de Tchebyshev :
- polycheby.py
#!/usr/bin/env python # -*- coding: utf-8 -*- """ graphes de Polynomes de Chebyschev """ from math import * from pylab import * def polyeval(x,a): """ application de l'algorithme de Horner cf. http://fr.wikipedia.org/wiki/M%C3%A9thode_de_Ruffini-Horner """ n = len(a)-1 # n = ordre du polynome p = 0. for i in range(n,-1,-1): p = p * x + a[i] return p def polyscal(s,a): """ polynôme multiplié par un scalaire s """ b = [] for coef in a: b.append(coef*s) return b # on retourne les coefficients multipliés par s def polyshift(a): """ Multiplication du polynôme par la variable x """ b = [0] + a # cela revient à "shifter" la liste des coefficients en insérant un 0 "à gauche" return b def polyadd(a,b): """ Addition de deux polynômes de coefficients a et b """ r = a[:] # on travaille sur une copie de a pour ne pas le modifier t = b[:] # idem pour b g = [] # polynôme somme n1 = len(r) # ordre du premier polynôme n2 = len(t) # ordre du second polynôme if n1 > n2: # premier polynôme de plus haut degré que le second for i in range (n1-n2): t.append(0) elif n1 < n2: # second polynôme de plus haut degré que le premier for i in range (n2-n1): r.append(0) # r et t ont à présent la même longueur for i in range (len(r)): g.append(r[i]+t[i]) return g # on retourne les coefficients additionnés dans la liste g def polycheby(nmax): """ Fonction générant les coefficients des polynômes de Tchebyshev jusqu'à l'ordre nmax cf. http://fr.wikipedia.org/wiki/Polyn%C3%B4me_de_Tchebychev pour la formule de récurrence """ rep = [[1.], [0.,1.]] # les deux premiers polynômes (degrés 0 et 1) pour l'application de la formule de récurrence if nmax < 1: # si nmax est inférieur au degré 1, on renvoie le polynôme de degré 0 rep=[[1.]] if nmax > 1: # pour le degré max supérieur à deux, on calcule les polynômes suivants for n in range(2,nmax+1): # P_n(x) = 2 x P_n-1(x) - P_n-2(x) rep.append(polyadd(polyscal(2.,polyshift(rep[n-1])),polyscal(-1.,rep[n-2]))) return rep # utilisation des objets numpy x = arange(-1.,1.00001,0.01) chebs = polycheby(10) # quelques premiers polynômes de Tchebyshev print(chebs) # création des graphes de tous ces polynomes for pol in chebs: print(pol) plot(x,polyeval(x,pol)) axis([-1,1,-1,1]) # xmin, xmax, ymin, ymax title('Polynomes de Tchebyshev') legend() show()
À ce stade, il est utile de s'exercer avec d'autres familles de polynômes orthogonaux qui interviennent dans de nombreuses applications de la mécanique quantique.
De plus, des modules de calcul scientifique utilisant les familles classiques de polynômes orthogonaux existent dans NumPy. Leur mise en œuvre nécessite simplement l'étude de la documentation et d'exemples.