Rotateur biatomique
Cf. cette page.
Code source, en Python 3 :
- rotateur_biatomique-02.py
#!/usr/bin/env python # -*- coding: utf-8 -*- """ Somme d'état (ensemble canonique) de rotation (rotateur biatomique) Les impressions sont à récrire avec l'instruction format() de python 3 """ from math import exp # on a juste besoin de l'exponentielle import matplotlib.pyplot as plt # directive d'importation standard de Matplotlib T = 100. # (température réduite = T / Theta) Zrot = 0. # somme d'état Jmax = 30 # valeur maximale de J print('---------------------------------------------------') print('| J | dégénerescence | J*(J+1) | terme de Z |') print('---------------------------------------------------') Js=[] terms=[] for J in range(Jmax+1): g = 2*J+1 # dégénerescence term= (2*J+1)*exp(-J*(J+1)/T) print('| %3d | %4d | %4d | %.8e |' % (J, g, J*(J+1), term)) Zrot += term Js.append(J) terms.append(term) print('---------------------------------------------------') print( "Somme d'état à T=%3d jusqu'au niveau %2d : %.8e " % (T,Jmax,Zrot)) fig = plt.figure() plt.title(u"Rotateur biatomique et somme d'état à T = "+str(T)) plt.plot(Js, terms, 'bo', label=r'$(2J+1)\exp{(-J(J+1)\theta_{rot}/T)}$') plt.legend(loc='upper right') plt.vlines(Js, [0], terms) plt.xlabel(u"Niveaux J") plt.ylabel(u"Termes de la somme d'état") eq = r'$Z_I^{Rot} = \sum_{J} (2J+1) \exp{(-J(J+1)\theta_{rot}/T)} = '+str(round(Zrot,3))+"$" size = 14 x,y = 12,7 plt.text(x, y, eq, fontsize=size, clip_on=True) plt.show() # vue interactive de la figure
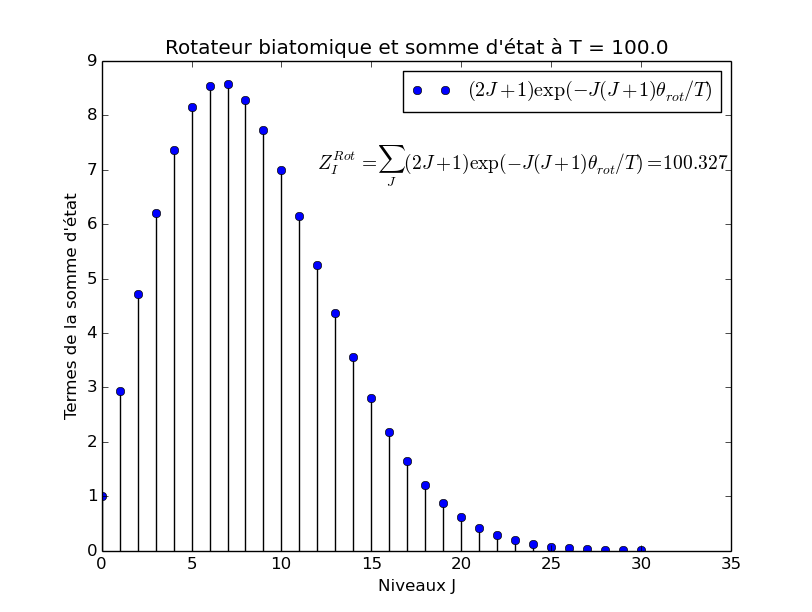
Figure :
Sortie des valeurs :
--------------------------------------------------- | J | dégénerescence | J*(J+1) | terme de Z | --------------------------------------------------- | 0 | 1 | 0 | 1.00000000e+00 | | 1 | 3 | 2 | 2.94059602e+00 | | 2 | 5 | 6 | 4.70882267e+00 | | 3 | 7 | 12 | 6.20844306e+00 | | 4 | 9 | 20 | 7.36857678e+00 | | 5 | 11 | 30 | 8.14900043e+00 | | 6 | 13 | 42 | 8.54160866e+00 | | 7 | 15 | 56 | 8.56813596e+00 | | 8 | 17 | 72 | 8.27478835e+00 | | 9 | 19 | 90 | 7.72482354e+00 | | 10 | 21 | 110 | 6.99029276e+00 | | 11 | 23 | 132 | 6.14411195e+00 | | 12 | 25 | 156 | 5.25340178e+00 | | 13 | 27 | 182 | 4.37469528e+00 | | 14 | 29 | 210 | 3.55123642e+00 | | 15 | 31 | 240 | 2.81225655e+00 | | 16 | 33 | 272 | 2.17386690e+00 | | 17 | 35 | 306 | 1.64106933e+00 | | 18 | 37 | 342 | 1.21036009e+00 | | 19 | 39 | 380 | 8.72460102e-01 | | 20 | 41 | 420 | 6.14818650e-01 | | 21 | 43 | 462 | 4.23670231e-01 | | 22 | 45 | 506 | 2.85550178e-01 | | 23 | 47 | 552 | 1.88274853e-01 | | 24 | 49 | 600 | 1.21458857e-01 | | 25 | 51 | 650 | 7.66753988e-02 | | 26 | 53 | 702 | 4.73727511e-02 | | 27 | 55 | 756 | 2.86481384e-02 | | 28 | 57 | 812 | 1.69591336e-02 | | 29 | 59 | 870 | 9.82856285e-03 | | 30 | 61 | 930 | 5.57687812e-03 | --------------------------------------------------- Somme d'état à T=100 jusqu'au niveau 30 : 1.00327380e+02