Optimisation de la température caractéristique du diamant suivant le modèle d'Einstein
Ce modèle prévoie la dépendance à la température de la capacité calorifique d’un solide cristallin.
La détermination de la température caractéristique nécessite de “fitter” les données expérimentales en suivant une relation impliquant un paramètres qui sera optimisé pour minimiser la somme des carrés des écarts entre les valeurs modélisées et les valeurs expérimentales.
Le programme Python nécessite les librairies scipy (optimisation), numpy (manipulation des données) et matplotlib (représentation du fit).
<sxh python; title : fit-Cv-diamant-Einstein-04.py> #!/usr/bin/env python # -*- coding: utf-8 -*- “”“ Fit des données (température absolue, chaleur spécifique molaire à volume constant Diamant Modèle d'Einstein : http://fr.wikipedia.org/wiki/Mod%C3%A8le_d%27Einstein ”“” import numpy as np import scipy as sp from scipy.optimize import leastsq import matplotlib.pyplot as plt
def cvEinstein(Tr):
# fonction à fitter # Tr = température réduite = T/TE return 3.*NA*kB*(1./Tr)**2*sp.exp(1./Tr)/(sp.exp(1./Tr)-1)**2
def residuals(p,x,y):
# erreur entre y donné et y calculé return cvEinstein(x/p[0]) - y
kB = 1.3806488E-23 # Constante de Boltzmann NA = 6.02214129E23 # Nombre d'Avogadro # données expérimentales (T, Cv) : liste_data=[ [12.9,0.00053], [16.1,0.00081], [19.8,0.00138], [24.1,0.00257], [30.1,0.00494], [33.4,0.0074], [41.3,0.0133], [47.7,0.02], [57.2,0.0365], [67,0.0595], [76.1,0.092], [87,0.147], [100.4,0.24], [113.1,0.378], [126.3,0.56], [143.4,0.88], [159,1.19], [176,1.66], [197,2.21], [215,2.61], [264,4.18], [273,5.2], [280,5.43], [306,6.59], [335,7.81], [363,9.02], [412,11.8], [471,14.6], [516,15.6], [874,22.3], [1079,22.4], [1238,22.7]]
# transformation en tableau numpy data=np.array(zip(*liste_data)) # cf. http://docs.python.org/2.7/library/functions.html#zip
p=[1000.] # valeur initiale de l'unique paramètre recherché (TE) plsq = leastsq(residuals, p, args=(data[0], data[1])) # fit par moindre carré # Résultat : print “Température caractéristique suivant le modèle d'Einstein: ”,plsq[0]
# graphe x=np.linspace(1.,1.5*plsq[0],200) plt.plot(x,cvEinstein(x/plsq[0]),data[0], data[1],'o') plt.title(u'Capacité calorifique du diamant : optimisation par moindre carré') #plt.legend(['Fit', 'Experimental']) plt.show() </sxh>
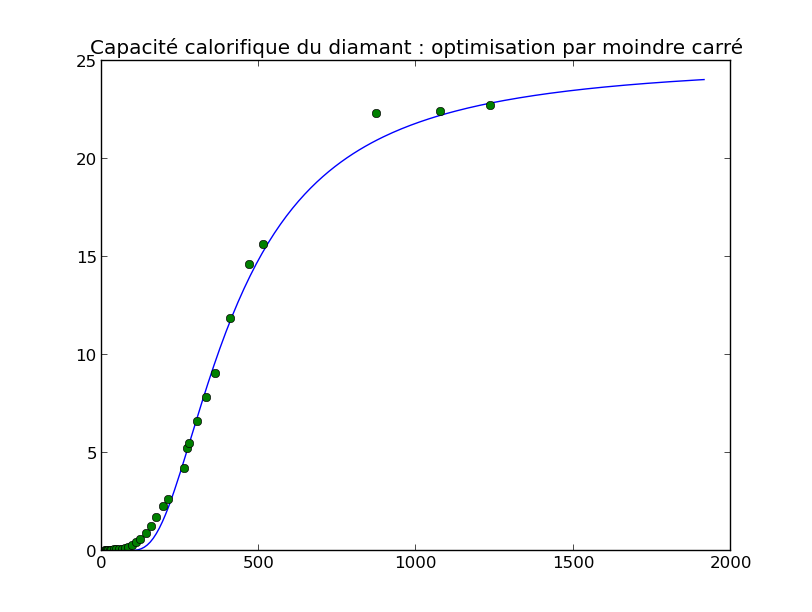
Le programme fourni comme température caractéristique pour le diamant 1275.76 K.
Voici la graphe obtenu :
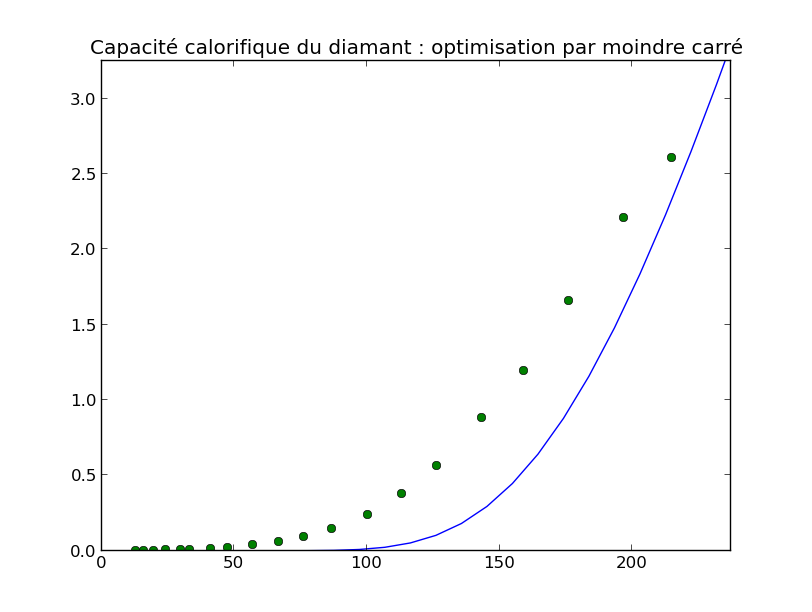
La zone à basse température pour laquelle on constate que le modèle d'Einstein n'est pas suffisamment correct :
Le modèle de Debye, qui utilise un spectre de fréquences plutôt qu'une fréquence unique de vibration, pourra remplacer le modèle d'Einstein. Le calcul nécessite d'utiliser les fonctions d'intégration scipy.integrate.quad, qui oblige de contourner l'utilisation des tableau numpy : les valeurs d'un tableau à traiter sont considérées une par une et le tableau numpy est recréé immédiatement. Voici un programme :
<sxh python; title : fit-Cv-diamant-Debye-02.py> #!/usr/bin/env python # -*- coding: utf-8 -*- “”“ Fit des données (température absolue, chaleur spécifique molaire à volume constant Diamant Modèle de Debye : http://fr.wikipedia.org/wiki/Mod%C3%A8le_de_Debye ”“” import numpy as np import scipy as sp from scipy.optimize import leastsq from scipy import integrate from scipy.integrate import simps import matplotlib.pyplot as plt
def f(x):
return x**4.*sp.exp(x)/(sp.exp(x)-1.)**2.
def cvDebye(Tr):
# Chaleur spécifique théorique (modèle de Debye)
# Tr = température réduite = T/TD
# problème : integrate.quad n'accepte pas le broadcast pour les limites a, b
# http://newscentral.exsees.com/item/12e4126a47e3411a138f5a3820eb62d1-71278f2740f3cd9c3dff2da0d78b6bc7
#solution :
if 'array' in str(type(Tr)):
return 9.*NA*kB*(Tr)**3 *np.array([integrate.quad(f,0,1./each_Tr)[0] for each_Tr in Tr]) # array
else:
return 9.*NA*kB*(Tr)**3 * integrate.quad(f,0,1./Tr)[0] # float
def residuals(p,x,y):
# erreur entre y donné et y calculé return cvDebye(x/p[0]) - y
kB = 1.3806488E-23 # Constante de Boltzmann NA = 6.02214129E23 # Nombre d'Avogadro # données expérimentales (T, Cv) : liste_data=[ [12.9,0.00053], [16.1,0.00081], [19.8,0.00138], [24.1,0.00257], [30.1,0.00494], [33.4,0.0074], [41.3,0.0133], [47.7,0.02], [57.2,0.0365], [67,0.0595], [76.1,0.092], [87,0.147], [100.4,0.24], [113.1,0.378], [126.3,0.56], [143.4,0.88], [159,1.19], [176,1.66], [197,2.21], [215,2.61], [264,4.18], [273,5.2], [280,5.43], [306,6.59], [335,7.81], [363,9.02], [412,11.8], [471,14.6], [516,15.6], [874,22.3], [1079,22.4], [1238,22.7]]
# transformation en tableau numpy data=np.array(zip(*liste_data)) # cf. http://docs.python.org/2.7/library/functions.html#zip
p=[1000.] # valeur initiale de l'unique paramètre recherché (TE) plsq = leastsq(residuals, p, args=(data[0], data[1])) # fit par moindre carré # Résultat : print “Température caractéristique suivant le modèle de Debye: ”,plsq[0]
# graphe x=np.linspace(1.,1.5*plsq[0],200) plt.plot(x,cvDebye(x/plsq[0]),data[0], data[1],'o') plt.title(u'Capacité calorifique du diamant : optimisation par moindre carré') #plt.legend(['Fit', 'Experimental']) plt.show() </sxh>